Verstandig fuseren
22 juni 2016 om 12:39 0 reacties
Sinds de jaren zestig heeft een groot aantal gemeentelijke herindelingen plaatsgevonden. In 1960 telden Nederland 1.151 gemeenten, in 2015 zijn dat er nog maar 393. Een van de beoogde doelen van herindelen is het profiteren van schaalvoordelen. Het is echter de vraag of er daadwerkelijk volop wordt geprofiteerd van de schaalvoordelen. Vaak is de schaal van de dienstverlening van gemeenten al te groot om nog te kunnen profiteren van schaalvoordelen.
Sinds de jaren zestig heeft een groot aantal gemeentelijke herindelingen plaatsgevonden. In 1960 telden Nederland 1.151 gemeenten, in 2015 zijn dat er nog maar 393. Een van de beoogde doelen van herindelen is het profiteren van schaalvoordelen. Het is echter de vraag of er daadwerkelijk volop wordt geprofiteerd van de schaalvoordelen. Vaak is de schaal van de dienstverlening van gemeenten al te groot om nog te kunnen profiteren van schaalvoordelen.
Wordt er inderdaad volop geprofiteerd van de schaalvoordelen? Allers en Geertsema (2014) laten zien dat de uitgaven na een herindeling niet dalen en dat het uitblijven van een uitgavendaling evenmin is toe te schrijven aan een verbeterd voorzieningenniveau.
Er is sprake van schaalvoordelen als de kosten per eenheid product afnemen door op grotere schaal te gaan produceren. Schaalvoordelen ontstaan omdat bij een grotere schaal het bijvoorbeeld mogelijk is de arbeidsverdeling beter te organiseren, een efficiënter gebruik van kapitaalgoederen te realiseren en met meer macht op de inkoopmarkt kwantumkortingen mogelijk te maken. Sowieso worden bij schaalvergroting de vaste kosten gedragen door een groter productievolume. Een toename van de schaal kan echter ook gepaard gaan met schaalnadelen. Een grotere gemeente heeft bijvoorbeeld te maken met meer bureaucratisering, minder sociale controle en een geringere betrokkenheid van ambtenaren bij de gemeente. Bij schaalvergroting is het dus altijd de vraag of de schaalvoordelen opwegen tegen de schaalnadelen.
De gemiddelde kosten hebben daarom dikwijls een zogenoemde U-vormig verloop. Eerst leidt schaalvergroting tot dalende gemiddelde kosten, de schaalvoordelen zijn sterker dan de schaalnadelen. Naarmate de schaal groter wordt, wordt het effect van de schaalvoordelen juist kleiner, daartegenover staat dat het effect van de schaalnadelen juist groter worden. Bij een bepaalde schaal wordt een omslagpunt bereikt, bij verdere schaalvergroting krijgen schaalnadelen de overhand en stijgen de gemiddelde kosten. Overigens is het niet altijd zo dat de gemiddelde kostencurve een U-vorm heeft. Het kan voorkomen dat schaalnadelen marginaal zijn. De gemiddelde kosten dalen dan tot een bepaald punt, waarna deze nagenoeg constant blijven, in een dergelijk geval hebben de gemiddelde kosten een L-vorm (zie figuur 1).
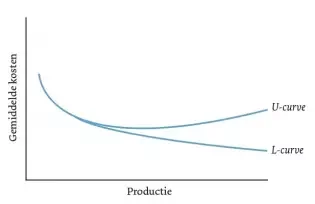
Figuur 1: Voorbeeld U-vormig en L-vormig verloop van de gemiddelde kosten
Schaaleffect en doelmatigheidseffect
Bij een fusie wordt de schaal van een gemeente in één klap fors uitgebreid en lijkt het mogelijk om op eenvoudige wijze van schaalvoordelen te profiteren. Echter bij een fusie komen ook fusiekosten om de hoek kijken. Deels betreft dit ondoelmatigheid die ontstaat door frictie binnen de nieuwe organisatie. Er zijn bij een fusie dus twee effecten waarmee rekening moet worden gehouden. In de eerste plaats schaaleffecten (economies of scale) en in de tweede plaats een ondoelmatigheidseffect (hogere kosten voor vergelijkbare dienstverlening). De omvang van beide effecten en de optimale schaal kunnen worden berekend met een grenskostenfunctie.
Fried et al. (2008) geven een vrij compleet overzicht van het modelleren van grenskostenfuncties en de verschillende schattingstechnieken. Een meer elementaire inleiding kan gevonden worden in Blank (2010). Het gebruik van de grenskostenfunctie heeft een enorm aantal wetenschappelijke artikelen opgeleverd met toepassingen. Een literatuuroverzicht met toepassingen voor de gemeentelijke dienstverlening wordt geven door Kalb (2010). Specifieke toepassingen voor de dienstverlening van Nederlandse gemeente worden bijvoorbeeld beschreven door Blank et al. (2011) over de gemeentelijke afvalinzameling, De Groot et al. (2014) over schaalvergroting bij gemeenten en recentelijk Niaounakis en Blank (2015) over de effecten van het gezamenlijk innen van de gemeentelijke belastingen.
Een kostenfunctie representeert de samenhang tussen enerzijds de kosten en anderzijds de omvang en samenstelling van de dienstverlening, de prijzen van de ingezette middelen (zoals ambtenarensalarissen) en de stand van de techniek. Uit de economische theorie volgt dat uit de kostenfunctie zogenoemde kostenaandelenfuncties zijn af te leiden (Färe & Primont, 1995). Deze kostenaandelenfuncties geven voor elk ingezet middel (bijvoorbeeld ambtenaren) de optimale relatie weer tussen de inzet van dat middel enerzijds, en de omvang en samenstelling van de dienstverlening, de prijzen van de ingezette middelen en de technische ontwikkeling anderzijds. Met andere woorden, de kostenfunctie beschrijft of verklaart de kosten, de kostenaandelenfuncties beschrijven of verklaren de samenstelling van de ingezette middelen.
Uit een kostenfunctie is direct een maat af te leiden voor schaaleffecten, de schaalelasticiteit. De schaalelasticiteit geeft aan wat het effect is van een groei van de inzet van middelen op de groei van de productie. Een schaalelasticiteit van boven de 1 betekent dat de productie sneller groeit dan de inzet van middelen en dat dus sprake is van schaalvoordelen (een elasticiteit van bijvoorbeeld 1,1 betekent dat bij een groei van 1% van de ingezette middelen de productie met 1,1% toeneemt). Een schaalelasticiteit kleiner dan 1 betekent dat er sprake is van schaalnadelen. Bij een verdere schaalvergroting groeien de kosten sneller dan de productie. Bij een schaalelasticiteit van 1 is er sprake van schaalneutraliteit (1% extra middelen gaat gepaard met 1% extra productie). Bij een schaalelasticiteit van 1 is er sprake van een optimale schaal, er zijn dan immers geen schaalvoordelen te behalen door te krimpen of te groeien.
In de tweede plaats is het, door gebruik te maken van een techniek waarbij de grenskostenfunctie wordt bepaald, mogelijk om de zogeheten kostendoelmatigheid te bepalen. Een grenskostenfunctie is een functie die gegeven de productie de laagste kosten geeft. Figuur 2 toont een voorbeeld van een grenskostenfunctie (ook wel ‘frontier’ of ‘beste praktijk’ genoemd). In de praktijk produceert niet iedere gemeente tegen de laagste kosten, met andere woorden niet iedere gemeente ligt op de grenskostenfunctie. De punten A, B en B’ stellen de combinatie van kosten en productie van drie gemeenten voor. Gemeente A en B’ liggen op de grenskostenfunctie en zijn daarom kostendoelmatig. Gemeente B daarentegen ligt niet op de grenskostenfunctie en is daarom kostenondoelmatig. De omvang van de kostenondoelmatigheid wordt bepaald door de (relatieve) afstand tot de grenskostenfunctie te bepalen: met hoeveel procent minder kosten kan dezelfde hoeveelheid worden geproduceerd. Voor een uitgebreide toelichting op de grenskostenfunctie en de techniek op een grenskostenfunctie empirisch vast te stellen: zie Kumbhakar en Lovell (2000).
Verschillen in doelmatigheidsscore kunnen onderzocht worden door deze te relateren aan kenmerken van de gemeente. Zo kan er ook een vergelijking worden gemaakt tussen gefuseerde en niet-gefuseerde gemeenten. Veronderstel dat in figuur 2 gemeenten B en B’ een fusie voorstellen van twee gemeenten van omvang A (B en B’ zijn twee keer zo groot in productie als A). Gemeente B is een ondoelmatige versie van de fusie, niet alleen is de productie twee keer zo hoog als A ook de kosten zijn twee keer zo hoog. Gemeente B’ is de doelmatige variant van de fusie, de fusie ligt op de grenskostenfunctie. In de figuur is te zien dat de productie van B’ twee keer zo hoog is als die van A, maar dat de kosten dat zeker niet zijn. Gemeente B’ is een fusie waarbij volledig is geprofiteerd van schaalvoordelen en er geen ondoelmatigheidseffecten optreden.
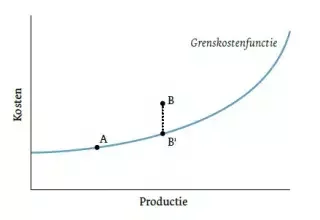
Figuur 2: Voorbeeld van een grenskostenfunctie en kostendoelmatigheid
Doelmatigheid wordt met een grenskostenfunctie vastgesteld en is een relatief begrip. Dat wil zeggen de doelmatigheid van een gemeente wordt bepaald door te vergelijken met andere gemeenten die zoveel mogelijk in dezelfde omstandigheden verkeren. Dat betekent dat doelmatigheid ongevoelig is voor veranderingen door de tijd heen. Als we bijvoorbeeld de doelmatigheid bepalen in twee verschillende periodes, dan wordt de doelmatigheid bepaald door gemeenten te vergelijken binnen dezelfde periode. Wordt het maken van een paspoort duurder doordat er vingerafdrukken in worden opgenomen, dan heeft dit geen effect op de doelmatigheid. Immers voor iedere gemeente wordt het maken van de paspoorten duurder.
Ook bij het vergelijken van groepen van gemeenten kan het relatieve karakter van de doelmatigheid een voordeel opleveren. Stel dat er geen correlatie is tussen de groepsindeling en een bepaald kenmerk dat van invloed is op de doelmatigheid. Dan heeft het kenmerk geen invloed op de resultaten van een vergelijking van groepen van gemeenten. Bijvoorbeeld, een veel gehoorde opmerking over doelmatigheidsonderzoek bij gemeenten is dat gemeenten op verschillende manieren kosten toerekenen. Dit kan inderdaad van invloed zijn op de doelmatigheid van een individuele gemeente. Maar bij het vergelijken van groepen van gemeenten is dit niet meer van toepassing, ervan uitgaande dat er geen correlatie is tussen de gehanteerde methode van toerekening en de groepsindeling.
Resultaten
Voor het empirisch vaststellen van een grenskostenfunctie zijn gegevens over productie en kosten nodig. Door de diversiteit aan gemeentelijke (soms lastig te kwantificeren) outputs is het niet eenvoudig om een kostenfunctie op gemeentelijk niveau te modelleren die recht doet aan die grote diversiteit. Door in te zoomen op specifieke dienstverlening van gemeenten wordt het een stuk eenvoudiger om de dienstverlening te vangen in een aantal specifieke producten. Burgerzaken is een onderdeel van de gemeentelijke dienstverlening waar de producten goed te meten zijn. Productie-indicatoren voor burgerzaken zijn het aantal afgegeven paspoorten, rijbewijzen, identiteitskaarten, uittreksels uit de gemeentelijke basisadministratie, uittreksels uit de burgerlijke stand en het aantal huwelijksvoltrekkingen.
In het model is de productie bij burgerzaken gerelateerd aan de kostengegevens afkomstig uit de gemeenterekeningen. Het verband tussen ingezette middelen en productie is de kostenfunctie. De grenskostenfunctie is geschat met een Stochastische Frontier Analyse. Een uitgebreide beschrijving van het gebruikte model en data is te vinden in Van Hulst en de Groot (2011).
Uit de geschatte kostenfunctie zijn direct de schaaleffecten af te leiden. Statistisch is getoetst of de schaalelasticiteit significant van 1 afwijkt (bij een elasticiteit van 1 is de schaal optimaal). Figuur 3 toont voor iedere gemeente of er bij burgerzaken sprake is van schaalvoordelen, schaalnadelen of een optimale schaal. Ongeveer 20% van de gemeenten heeft een omvang die rond de optimale schaal ligt.
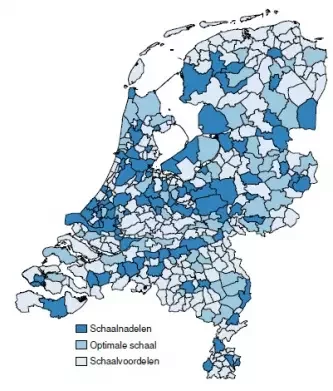
Figuur 3: Geschatte schaaleffecten bij burgerzaken 2012
Voor ruim 65% van de gemeenten gelden schaalvoordelen, deze gemeenten zouden dus baat hebben bij een groei. Het aantal gemeenten dat een te grote schaal heeft voor burgerzaken is 15%. Het omslagpunt waarbij schaalvoordelen omslaan in schaaldelen kent een bandbreedte van 17.000 tot 65.000 inwoners. Dat wil zeggen van de gemeenten waarvoor geen schaalvoordelen of schaalnadelen worden gevonden de kleinste 17.000 inwoners heeft en de grootste gemeente 65.000 heeft. Binnen die bandbreedte zijn er ook gemeenten waarvoor wel schaalvoordelen of schaalnadelen worden gevonden. Omgekeerd geldt wel dat alle gemeenten met minder dan 17.000 inwoners schaalvoordelen hebben en alle gemeenten met meer dan 65.000 inwoners schaalnadelen hebben.
Om inzicht te krijgen in de omvang van de effecten, zijn de te behalen schaalvoordelen gesimuleerd. Hiervoor is eerst een fictieve gemeente geconstrueerd die produceert op de optimale schaal. Voor de constructie van een fictieve gemeente wordt een aantal stappen genomen. Uit de resultaten van de kostenfunctie valt direct af te leiden welke gemeenten de optimale schaal hebben. Er zijn echter meerdere configuraties voor de optimale schaal mogelijk, het is immers onwaarschijnlijk dat iedere gemeente met een optimale schaal dezelfde samenstelling van productie heeft. Daarom zijn de gemeenten met een optimale schaal gesorteerd op schaalelasticiteit en is vervolgens de mediane waarneming geselecteerd. Vervolgens is berekend hoeveel maal we de productie van deze gemeente nodig hebben om dezelfde hoeveelheid te produceren als in de situatie waar nog schaalvoordelen te behalen zijn.
Daarna kunnen de kosten in de bestaande situatie en de fictieve situatie, waarbij op optimale schaal wordt geproduceerd, worden vergeleken. Voor gemeenten met een te kleine afdeling burgerzaken zijn de potentiële besparingen ongeveer 6%. Voor de gemeenten die werken op een schaal die te groot is, zijn de potentiële besparingen ongeveer 22%. De totale macrobesparingen, dat wil zeggen als iedere gemeente op optimale schaal produceert, kunnen worden berekend door het aandeel in de totale kosten van de te kleine en te grote gemeenten te vermenigvuldigen met de potentiële besparingen. De potentiële macrobesparingen zijn dan respectievelijk 1,5% voor de te kleine gemeenten en 13% voor de te grote gemeenten. Er zijn dus weliswaar veel gemeenten met een te kleine schaal, maar op macroniveau is de winst van schaalvergroting relatief klein door een klein kostenaandeel in de totale kosten.
Ook is nagegaan wat de effecten van de fusies in de praktijk zijn geweest. Allereerst is gekeken naar het schaaleffect. Daartoe is wederom gebruik gemaakt van een simulatie, dit keer voor burgerzaken van de fusiegemeenten in de periode 2007-2012.
Voor iedere fusie is in het jaar voorafgaand aan de fusie een fictieve fusie geconstrueerd. Zodoende zijn er in het jaar voorafgaand aan de fusie gegevens over de individuele gemeenten van een fusie en de bijbehorende fictieve fusiegemeente. Voor zowel de individuele gemeenten als de fictieve fusies zijn de verwachte kosten berekend met de grenskostenfunctie en met elkaar vergeleken. Het blijkt dat in de periode 2007-2012 de fusies gemiddeld 4,7 procent aan schaalvoordelen hebben opgeleverd.
In tweede plaats is nagegaan of er, naast schaaleffecten, ook nog sprake is van een doelmatigheidseffect. In een analyse is gekeken hoe de kostendoelmatigheid van gefuseerde gemeenten zich verhoudt tot die van de niet-gefuseerde gemeenten. De tabel toont de gemiddelde kostendoelmatigheid van de afdeling burgerzaken in 2006 en in 2012. De doelmatigheid in 2006 wordt gebruikt om te kijken of er wellicht voorafgaand aan een fusie al sprake is van verschillen in doelmatigheid, de doelmatigheid in 2012 wordt gebruikt om de verschillen in doelmatigheid na fusie in kaart te brengen.
Voor de niet (recentelijk) gefuseerde gemeenten is de gemiddelde kostendoelmatigheid van de afdeling burgerzaken in 2012 gemiddeld 88%. Voor een afdeling burgerzaken van een gemeente, ontstaan uit een gemeentelijk herindeling in 2007 of later, ligt de kostendoelmatigheid gemiddeld 6 procentpunt lager. Is de herindeling iets langer geleden, tussen 1999 en 2006, dan ligt de doelmatig gemiddeld nog steeds 4,5 procentpunt lager. Is de fusie nog langer geleden, dan is de gemiddelde doelmatigheid nog steeds lager, maar is het effect niet meer significant. Het effect van een herindeling op de doelmatigheidsscore lijkt dus langzaam weg te ebben.
Nu kan het natuurlijk zijn dat de fuserende gemeenten voorafgaand aan de fusie al een lagere kostendoelmatigheid hebben en de lagere doelmatigheidsscore geen gevolg is van de fusie. Daarom is eveneens nagegaan wat de doelmatigheidsscore is voorafgaand aan de herindeling. Daartoe is de doelmatigheidsscore in 2006 berekend en is gekeken in hoeverre de kostendoelmatigheid van gemeenten die in de periode 2007-2012 zijn gefuseerd, afwijkt. Het blijkt dat de gemiddelde kostendoelmatigheid in 2006 van een afdeling burgerzaken voorafgaand aan de fusie hoger ligt, het effect is overigens klein (gemiddeld 0,8 procentpunt) en zeker niet significant. Het is in ieder geval dus niet zo dat de ondoelmatigheid al bestond voorafgaand aan de fusie.
| Gemeente 2006 | Doelmatigheid | T-waarde | N |
| Geen fusie | 87,6 | 165,0 | 336 |
| Gaat fuseren na 2006 | 0,8 | 0,6 | 67 |
| Gemeente 2012 | Doelmatigheid | T-waarde | N |
| Geen fusie | 88,0 | 123,8 | 291 |
| Gefuseerd 2007-2012 | -6,0 | -2,3 | 24 |
| Gefuseerd 1999-2006 | -4,5 | -2,5 | 50 |
| Gefuseerd 1995-1998 | -2,0 | -1,1 | 50 |
Tabel: Gemiddelde doelmatigheid in 2006 en 2012 (in %)
Conclusie
Productie op de optimale schaal kan in potentie een paar procent besparing opleveren. Er is echter een aantal punten waar rekening mee moet worden gehouden.
In de eerste plaats is een optimale schaal niet synoniem met een grotere schaal. Bij een analyse van burgerzaken slaan schaalvoordelen vanaf een bepaalde omvang om in schaalnadelen. Bij een te grote omvang is juist het verkleinen van de schaal de stap richting de optimale schaal. Bovendien kunnen de besparingen van een schaalvergroting macro gezien tegenvallen. Bij burgerzaken zijn er weliswaar veel kleine gemeenten waar schaalvoordelen te behalen zijn, tegelijk is het zo dat juist omdat het kleine gemeenten betreft, het macro gezien om relatief kleine besparingen gaat.
In tweede plaats is er bij een schaalvergroting door fusie niet alleen een schaaleffect, maar ook een doelmatigheidseffect. Het kan hier bijvoorbeeld gaan om tijdelijke integratie-effecten, maar ook het blijven aanbieden van de diensten van burgerzaken op meerdere locaties in de fusiegemeenten. Daarnaast is het zo dat boventallig personeel na een fusie niet zomaar valt te ontslaan, vaak gaat aanpassen van het personeelsbestand via natuurlijk verloop. Het negatieve effect op de kostendoelmatigheid is de eerste jaren na fusie gemiddeld sterker dan de winst die behaald wordt uit schaalvergroting. Pas een aantal jaar na de fusie verbetert de kostendoelmatigheid en is er pas echt sprake van het volledig benutten van schaalvoordelen.
Tot slot zij het opgemerkt dat de hier gepresenteerde resultaten betrekking hebben op burgerzaken, dat is slechts een klein deel van de gehele gemeentelijke dienstverlening. De optimale schaal van burgerzaken zegt alleen iets over burgerzaken, niet over de gemeente als geheel. De Groot et al. (2014) laten zien dat voor afvalbeheer de optimale schaal rond de 65.000 inwoners ligt, terwijl pas bij meer dan 300.000 inwoner de schaalnadelen significant zijn. Niaounakis en Blank (2015) stellen dat voor gemeentelijke heffingen de optimale schaal pas bij 460.000 inwoners wordt bereikt. Kennelijk is het antwoord op de vraag of en in welke mate geprofiteerd kan worden van schaalvoordelen afhankelijk van het type dienstverlening. Wel is het altijd zo dat de schaalvoordelen vanaf een bepaald punt omslaan in schaalnadelen.
Over de tijdelijke transitiekosten is bij andere vormen van dienstverlening niets bekend. Maar aangezien Allers en Geertsema (2014) laten zien dat de uitgaven na een herindeling niet dalen, is het aannemelijk dat bij andere vormen van dienstverlening ook sprake is van transitiekosten.
Verder is de schaal hier bezien vanuit een economisch perspectief. Over andere aspecten, zoals bestuurlijke, ambtelijke en financiële slagkracht, die ook in de overwegingen van een fusie een rol kunnen spelen, worden geen uitspraken gedaan.
Bart van Hulst is onderzoeker aan de TU-Delft.
Jos Blank is hoogleraar aan de Erasmus Universiteit te Rotterdam en directeur van het Centrum voor Innovaties en Publieke Sector Efficiëntie Studies (IPSE Studies |CAOP-TU Delft-EUR).
Literatuur
- Allers, M.A., & Geertsema, B. (2014), ‘Geen grotere doelmatigheid door herindeling gemeenten’, ESB, 99(4688), pp. 406-409.
- Blank, J., Felsö, F., & Groot, H. de (2011), ‘Beter Benchmarken’. TPC, 9(6), p. 5.
- Blank, J.L.T. (2010), Principes van productiviteitsmeting. Elementaire handleiding voor kwantitatief onderzoek naar de productiviteit, doelmatigheid, effectiviteit en kwaliteit van de publieke sector, Maastricht: Shaker Publishing B.V.
- Färe, R., & Primont, D. (1995), Multi-Output Production and Duality: Theory and applications, Dordrecht: Kluwer Academic Publishers.
- Fried, H.O., Lovell, C.A.K., & Schmidt, S.S. (2008), The measurement of productive efficiency and productivity growth, New York: Oxford University Press.
- Groot de, H., Hulst, B.L. van, & Wilschut, J. (2014), ‘De kostenvoordelen van schaalvergroting bij gemeenten’, ESB, 99(4678), p. 3.
- Hulst, B.L. van, & Groot, H. de (2011), Benchmark Burgerzaken, Een empirisch onderzoek naar de kostendoelmatigheid van burgerzaken, Delft: IPSE-Studies research reeks.
- Kalb, A. (2010), Public Sector Efficiency. Applications to local governments in Germany, Ph.D., Heidelberg: Universität Heidelberg. (ISBN 978-3-8349-2334-9)
- Kumbhakar, S.C., & Lovell, C.A.K. (2000), Stochastic frontier analysis, New York: Cambridge University Press.
- Niaounakis, T.K. & Blank, J.L.T. (2015), ‘Gerichte gemeentelijke samenwerking beter dan fuseren’, TPC, augustus 2015, pp. 4-8.
